Cascading 3.0 Query Planner

Original post: https://www.cascading.org/2014/09/18/the-cascading-3-0-query-planner/

Cascading 1.0 when released, represented a huge milestone. An enterprise friendly Java API, not a syntax, and fail fast planner allowed developers to build robust, maintainable, data-oriented applications that could execute reliably on Apache Hadoop for hours or days.

Cascading 2.0 made a nod towards cluster platform independence with the addition of an in memory ‘local’ mode that proved applications could be built without direct API access to the underlying platform. This provided much needed isolation across the evolving Hadoop platform and improved developer experience. Write once, run on any vendor provided platform.

Cascading 3.0 proves we can abstract away the underlying platform by providing additional platforms users can execute against, not just MapReduce. Apache Tez is the first such addition. Tez is the latest parallel computation fabric from the Apache group. It builds on Hadoop, keeping the Hadoop File System for instance, but uses a model that removes inefficiencies that are baked into the MapReduce model.

But we should point out the Cascading 3.0 abstraction is not just over the platform APIs, but also the semantics of the given platform like MapReduce or a DAG like model (like the one provided by Apache Tez). This is achieved by the Cascading “query planner”, it maps from one model to another.

Another way to restate this is that the Cascading query planner is not ‘mapping’ MapReduce onto other models, but mapping the Cascading model directly onto the underlying platform model, be it MapReduce or a DAG representation.

This makes the Cascading object model and their associated semantics an Intermediate Representation (or Intermediate Language) for data parallel cluster computing. Where new models can be created on top, over Cascading, and new ones can be mapped below, underneath Cascading. All the while retaining the qualities of both. LLVM provides this functionality to the compiler world. For example, Clang’s C, C++, and Objective-C; the Julia language (a technical computing language); and the Swift language from Apple all rely on the LLVM provided Intermediate Representation (IR).

To keep things less ivory tower, we usually call Cascading a framework.

But in practice, Cascading as an IR is quite common. Cascading is the basis for Lingual, Pattern, Scalding, and Cascalog, each of which are higher order syntaxes or languages that are feature rich, reliable, and very useful unto themselves. Cascading is also being embedded in a number of commercial products that expose a different (more vertical) model to the end user.

How is this done? In large part, it’s due to the brand new query planner we have spent the balance of this year developing and testing. First with our ‘local’ mode and the MapReduce model, which were made available earlier this year in a Cascading 3.0 WIP release. And during the last couple of months, adding more degrees of freedom to support a model with, well, more degrees.

We could have just used the MapReduce planner directly on Tez, but the point of the DAG model in Tez is to remove the inefficiencies inherent to MapReduce. For example, no more ‘identity mapper’; added support for multiple outputs; no prefixing data with join ordinality; suppressing sorting when not needed; removing HDFS as an intermediate store between jobs; etc.

Over the years we realized we need to rethink how the prior planners mapped Cascading into new platform models, but more importantly, how we can move control of adding new Cascading primitives, optimizations, or whole new platforms back to the Cascading user. The answer was somewhat obvious when looking at similar systems — create a rule language users can use to create rules and to create new rule sets.

But there are some reasonably complicated difficulties we had to address. Recognizing that what a Cascading user creates is itself a DAG (Directed Acyclic Graph) of elements that the user would like to execute remotely is key.

From there, the key difficulties we had to address boiled down to:

• Allowing rules to be abstract enough so that they can target patterns of nodes and edges in the user DAG without having to account for all possible permutations
• Isolating the structural and compatibility testing of the target DAG from the structural transformation of the DAG
• Allow for high levels of code reusability
• Allow rules to offer syntactic context on errors
• Allow rules to leverage all available meta-data, including the structural qualities of the DAG itself
• Present a simple ‘language’ that allows users to develop custom rules

Most of the above translates to having “rules” that can assert a DAG is a valid structure, transform a DAG into a new DAG, or partition a DAG into sub-DAGs.

In terms of MapReduce, we want to define rules that verify aggregations always follow a grouping; identify and group “map” side and “reduce” side elements; insert temporary files between the “reduce” side elements and the “map” side elements; break the graph up into physical jobs.

The root of the solution is to rely on a way to match sub-DAGs (or sub-graphs) within a larger graph. That is, we need a regular expression like “language”, not for strings and text, but for graphs of nodes and edges. In the literature this is called Sub-Graph Isomorphism Matching.

So we created what we call the Expression Graph API, a basis for building higher order complex logic allowing us to reason about or manipulate large complex graphs.

Fundamentally what we have is an API that allows a ‘match graph’ (think regular expression string) to be constructed that then can be applied to a larger graph to see if there is a match or, more generally useful, similarity between both structures. And if so, we can then perform an Assertion, Transformation, or Partition against the matched elements.

Consider the expression graph below, a simple DAG of two elements with some meta-data:

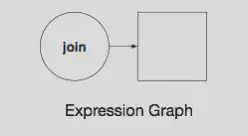
It will match the following elements in gray and not those with a dotted outline.

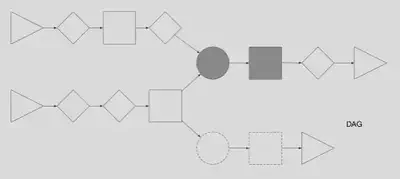
The above expression graph knows it is looking for a circle that is also a ‘join’ between two incoming elements. If there is no ‘join’, then don’t match.

But the world isn’t that simple. We had to go further to allow for matching of sub-graphs of distinguished elements.

That is, some elements in a graph can be ignored in a given case, but not in others. Thus the elements that matter, the distinguished elements, must be the only ones that match the graph expression. But the transformation must be applied to the full sub-graph bound by any matched distinguished elements.

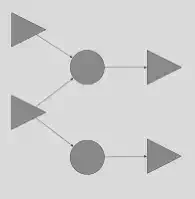
Consider the following expression graph, a circle or a triangle will match:

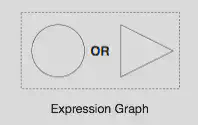
It will match the gray elements in the following graph:

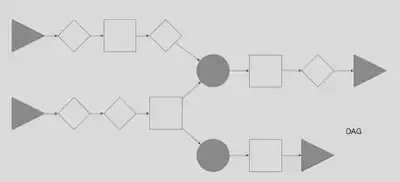
These would be the distinguished elements. Matching them allows us to remove all the other elements, or actually, mask them from subsequent matches, resulting in a contracted graph of the form:

Now we can apply a new expression graph (not shown) to find our target sub-graph of distinguished elements, the result is as follows:

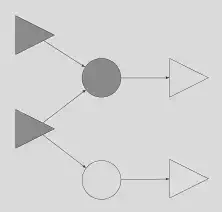
If we isolate the new sub-graph, above in gray, we can expand it to include it original intermediate nodes and edges, that is, unmask previously masked elements.

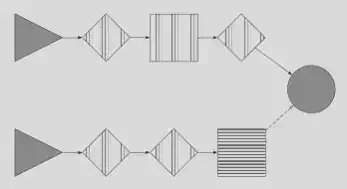
Finally we can provide yet another expression graph to assert or transform this final graph within the original full graph. In the graph above, we could provide a new expression graph looking for a square with horizontal lines, and if found we an insert a new element after it, along the dotted edge.

Alternately, we can extract the new sub-graph from the full original graph effectively letting us partition the larger graph into smaller ones.

We have only touched on the basics, but the language is still evolving while already quite powerful.

One last value of having assertions, transformations, and partitioning implemented as basic building blocks for re-usability; users can create new “rule sets” to optimize specific applications, or create a set of “rule sets” with a voting strategy to choose the best resulting execution plan based on cost or some other metric.